Machine-precise Verification of Simulink Models
In this post we show how to use Intrepyd (repo) to translate and verify MathWorks Simulink models. The translation is such that the semantic is machine-precise, i.e., we verify properties by taking into account finite integers and floating-point representations for integers and single or double precision variables, which is something that, at the time of writing this post, is not available even in Simulink Design Verifier, the verification tool that comes packaged with Simulink. We discuss how such precision is critical by reporting on a real-life software failure.
Highlights
- Brief introduction to Simulink
- Use Intrepyd to simulate Simulink specifications
- Use Intrepyd to verify Simulink specifications, also with floating-point interpretations
- The Patriot Missile failure
Keywords
Simulink, model-checking, model-based design
Installing Intrepyd
As of version 0.5.13, Intrepyd releases are pushed onto the PYPI archive, and it can be installed by simply issuing the following command
pip install intrepyd
The Simulink modeling language
Simulink is a graphical modeling language for control engineering. Together with SCADE, it is the market leader in model-based design, and a standard de-facto across avionics and automotive companies. In Simulink it is possible to specify controls having continuous or discrete time semantics. In this post we restrict our attention to the discrete part, which is also the subset that can be effectively tackled with symbolic verification techniques.
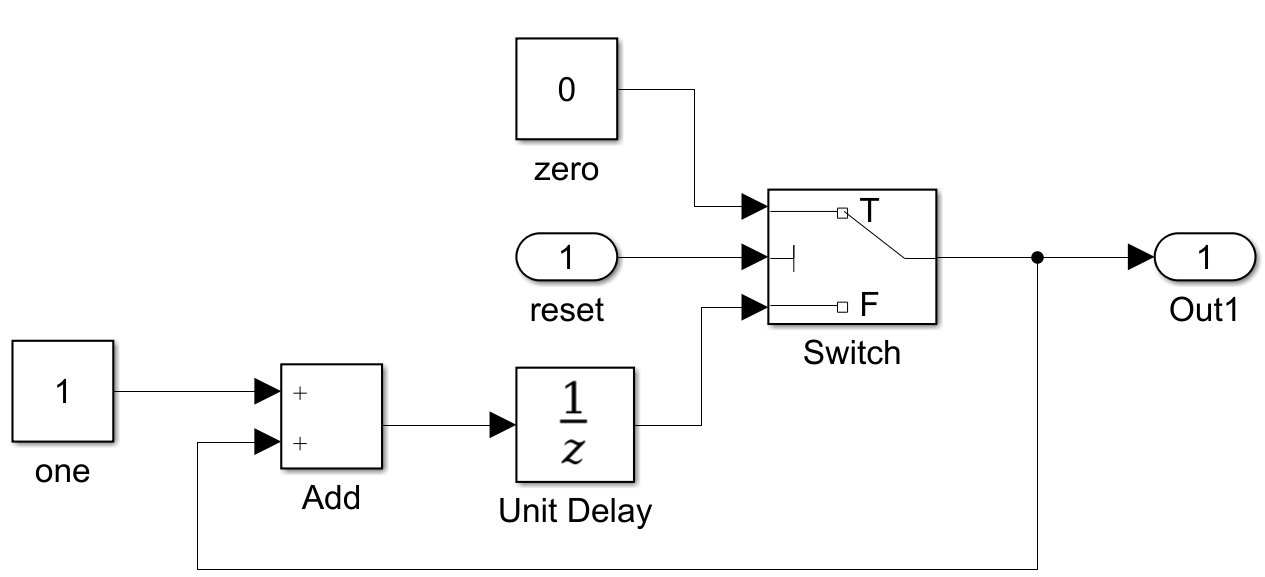
The following example, counter.slx shows a simple integer counter with a reset,
initialized to 0 and incremented by 1 at each clock tick:
Analyzing Simulink with Intrepyd
Simulation
Intrepyd can simulate the above model, using default values for the inputs with the following script
import intrepyd
import intrepyd.tools as ts
def doMain():
# Creates an intrepyd context
ctx = intrepyd.Context()
# Translates a simulink model into an instance of type
# SimulinkCircuit, which is created on the fly
circ = ts.translate_simulink(ctx, 'counter.slx', 'real')
# The method mk_circuits() loads the circuit into the context
circ.mk_circuit()
# Retrieve the nets corresponding to the outputs
outputs = [item[1] for item in circ.outputs.items()]
# Perform 10 steps of simulation, and store the result into 'counter.csv'
ts.simulate(ctx, 'counter', 10, outputs)
if __name__ == "__main__":
doMain()which can be executed as follows
$ python simulate.py
Simulating using default values into counter.csv
Simulation result written to counter.csv
0 1 2 3 4 5 6 7 8 9 10
reset F F F F F F F F F F F
counter/Switch 0 1 2 3 4 5 6 7 8 9 10thus producing the expected result (in particular the reset never triggers,
and so the counter value keeps increasing). It is possible to change the
default value for the input at any step by editing counter.csv, the byproduct
of simulation. For instance by setting reset to true at step 6 we obtain
the following resimulation
$ python simulate.py
Re-simulating using input values from counter.csv
Simulation result written to counter.csv
0 1 2 3 4 5 6 7 8 9 10
reset F F F F F F T F F F F
counter/Switch 0 1 2 3 4 5 0 1 2 3 4which shows the expected behavior.
Notice that Intrepyd translates and operates on a Simulink design without the need of an active session of Matlab. In fact no Matlab installation is even necessary on the running machine, thus allowing vitually infinite instances of Intrepyd to be run in parallel on local machines, remote servers, or clusters.
Verification
(An introduction to verification can be found in a previous post.)
We extend the counter.slx model with an invalid property into a new model counter_verify.slx:

The property is invalid because, if the reset never triggers, at step 6 the counter value becomes greater than 5. We can verify the property with the following script
import intrepyd
import intrepyd.tools as ts
def doMain():
ctx = intrepyd.Context()
circ = ts.translate_simulink(ctx, 'counter_verify.slx', 'real')
circ.mk_circuit()
# Iterates throughout all the targets, which are nets corresponding
# to the negation of properties
for target in circ.targets:
print 'Processing proof objective:', target
# Creates a Backward Reachability engine
br = ctx.mk_backward_reach()
target_net = circ.targets[target]
# Inform the engine to reach 'target_net'
br.add_target(target_net)
# Inform the engine to track 'target_net' in the counterexample
# Only input values are tracked automatically
br.add_watch(target_net)
result = br.reach_targets()
print result
if result == intrepyd.engine.EngineResult.REACHABLE:
# Retrieves the counterexample, aka trace
trace = br.get_last_trace()
# Transforms the trace into a 'pandas' dataframe
dataframe = trace.get_as_dataframe(ctx.net2name)
print dataframe
if __name__ == "__main__":
doMain()that can be executed as follows
$ python verify.py
Processing proof objective: counter_verify/Proof Objective
EngineResult.REACHABLE
0 1 2 3 4 5 6
reset ? F F F F F F
NOT counter_verify/Proof Objective F F F F F F Twhich is a counter-example for the property (notice that internally we negate the property to turn it into what we call a target, and so it appears negated in the trace too).
Machine-precise verification
Let’s have a look to another example, where we have explicitly shown the port datatypes:
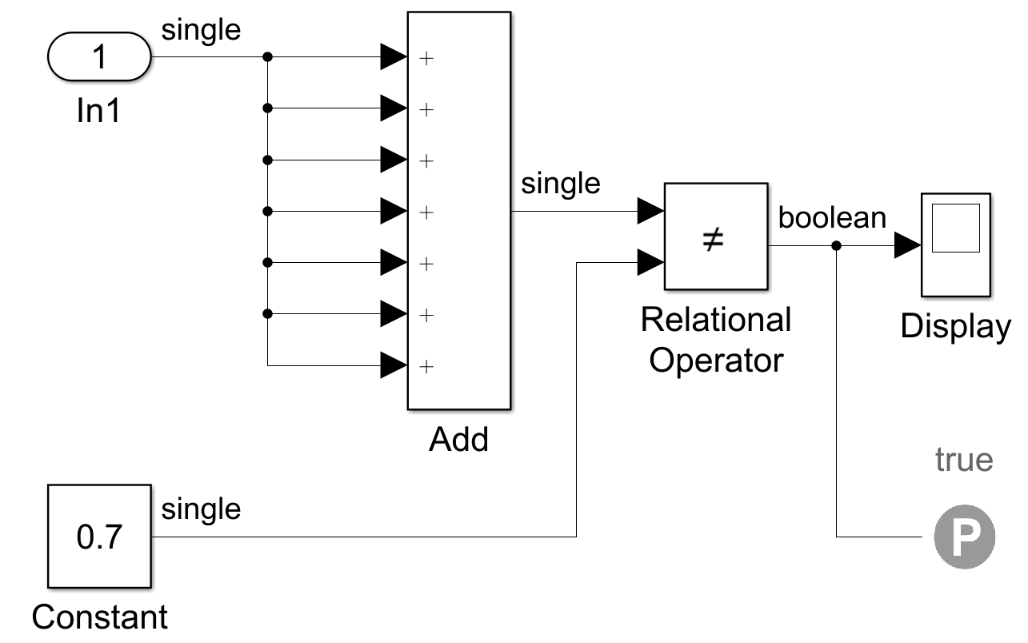
The model can be seen as an encoding for the equation 7x = 0.7. So one
is tempted to say that a solution is x = 0.1. Simulink Design Verifier (SLDV)
is the verification tool that is provided by MathWorks to prove or disprove
properties in a Simulink design. In this case SLDV is able to disprove the
property, and it indicates exactly x = 0.1 as a suitable solution.
But is that really a solution ? Let’s take a small modification of the
model, where we replace the input (x) with the constant value 0.1. If
we now run a simulation we will find out that the property is in fact
not violated (as the display shows a 1):
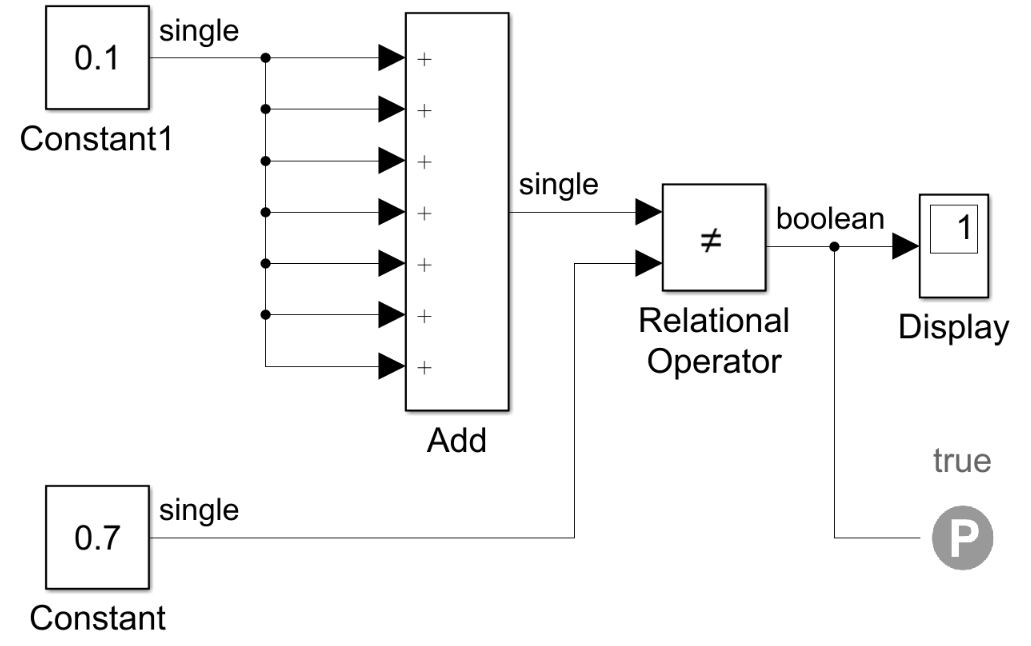
therefore SLDV disagrees with the simulation.
OUCH !
First of all, who is right ? Simulation is right, because in floating-point
arithmetic 0.1 cannot be represented precisely (it is a periodic number, pretty much
as 1/3 in base 10) and it is subjected to an approximation. Therefore when summing
a sufficiently large amount of 0.1s the error accumulates, and 7 sums are enough
to turn a 0.7 into a 0.69....
So what’s wrong with SLDV ? SLDV works on an approximated interpretation of the model, i.e., it interprets floating-point numbers as infinite-precision rationals, that are not subjected to approximation errors, making the reasoning not faithful with floating-point architectures, which are those on which the code will eventually run. This known problem is also reported by a warning upon calling SLDV.
Intrepyd instead supports both rational and floating-point reasoning. The following script attempts to prove the property with reals and floating points.
import intrepyd
import intrepyd.tools as ts
import time
def doMain(sort):
print '**** Solving with', sort, '****'
ctx = intrepyd.Context()
circ = ts.translate_simulink(ctx, 'float_vs_real.slx', sort, sort + '_')
circ.mk_circuit()
for target in circ.targets:
br = ctx.mk_backward_reach()
target_net = circ.targets[target]
br.add_target(target_net)
br.add_watch(target_net)
result = br.reach_targets()
print result
if result == intrepyd.engine.EngineResult.REACHABLE:
trace = br.get_last_trace()
dataframe = trace.get_as_dataframe(ctx.net2name)
print dataframe
if __name__ == "__main__":
doMain('real')
print
doMain('float')The execution shows that the encoding with reals is reporting the same result as SLDV, while the encoding with floating-points reports that no solution is possibile.
$ python verify_2.py
**** Solving with real ****
Simulink file float_vs_real.slx translated as real_.py
EngineResult.REACHABLE
0
In1 0.100000
**** Solving with float ****
Simulink file float_vs_real.slx translated as float_.py
EngineResult.UNREACHABLEWe have to point out that Floating-point verification is much slower than verification using reals (about 4x slower in this example): the price to pay for correctness.
Anyways, if you think that the example that we have just proposed is a bit artificial, please continue reading the following section.
The Patriot Missile Failure
The following story has been taken (and shortened) from here.
In 1991, during the Gulf War, an American Patriot missile failed to intercept
an Iraqi Scud missile, which eventually killed 28 soldiers. The reason for the
failure was an inaccurate calculation of the time by the computer software. In
particular the time measured by the clock in tenths of seconds since boot was multiplied
by 0.1 to get the time in seconds. The result was stored in a 24-bits register,
after an inevitable chopping (as we have seen 0.1 can’t be represented precisely
in binary). The resulting error is such that after 100 hours of boot time, the
difference in real and computed time is of 0.34 s, enough for the Scud to
escape the Patriot tracking range. Quoting the GAO report
[...]
Consequently, performing the conversion after the Patriot has been running
continuously for extended periods causes the range gate to shift away from
the center of the target, making it less likely that the target, in this
case a Scud, will be successfully intercepted.
[...]
Conclusion
We have shown the use of Intrepyd for the verification of Simulink designs, showing that it can deal with floating-point arithmetic when proving properties. We have highlighted the importance of such reasoning by reporting on a real software failure scenario. The scripts used in this post are available here.